On considère l'espace vectoriel E des polynômes à m variables, de degré
total au plus 1, à coefficients dans
![]() .
.
E étant isomorphe à
![]() , on notera
, on notera
![]() .
.
Soit
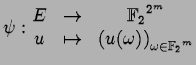 morphisme injectif,
on prend
morphisme injectif,
on prend
![]() Im
Im ![]() .
C est donc de longueur
.
C est donc de longueur ![]() , de dimension m+1.
De plus, on a
, de dimension m+1.
De plus, on a
![]() ,
,
![]() .
.