Soit
![]() ,
,
![]() .
Il faut trouver
.
Il faut trouver
![]() tel que
tel que
![]() soit minimale. Posons déjà
soit minimale. Posons déjà
![]() et
et
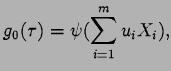 |
|
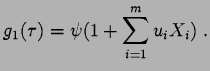 |
En posant
![]() ,
,
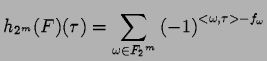
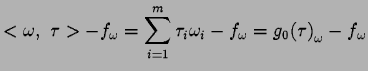
On a donc
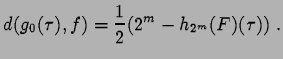
De même, on obtient
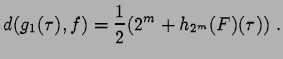
Il suffit donc de trouver
![]() tel que
tel que
![]() soit maximal.
soit maximal.
Ensuite, si
![]() , il faut choisir
, il faut choisir ![]() , c'est-à-dire prendre
, c'est-à-dire prendre ![]() .
Sinon,
.
Sinon, ![]() convient, c'est-à-dire
convient, c'est-à-dire ![]() .
.