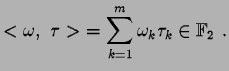
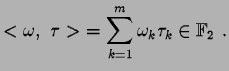
On note
![]() , qui a pour base
, qui a pour base
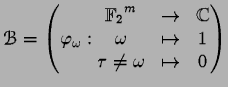 ,
et qui est donc de dimension
,
et qui est donc de dimension ![]() .
.
On pose alors pour
![]() ,
,
![]() ,
,
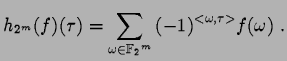
On remarque que
![]() ,
, ![]() est donc un
opérateur linéaire bijectif sur
est donc un
opérateur linéaire bijectif sur
![]() qui ressemble à une transformation de
Fourier discrète.
qui ressemble à une transformation de
Fourier discrète.
![]() est appelée la transformée
d'HADAMARD de f.
est appelée la transformée
d'HADAMARD de f.