A priori, le nombre d'additions de nombres complexes effectuées
pour calculer la transformée d'HADAMARD d'une fonction
![]() est en
est en ![]() .
.
Cependant, en notant ![]() la matrice de
la matrice de ![]() dans la
base
dans la
base
![]() , on peut remarquer que
, on peut remarquer que
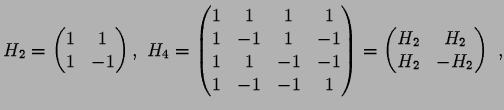
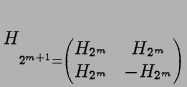 ,
soit
,
soit
Ainsi, le calcul de
![]() est ramené au calcul de
est ramené au calcul de
![]() .
.