let hadamard f=
let g=copy_vect f in
let rec hadam j n=
for k=0 to n-1 do
let aux=g.(j+k) in
g.(j+ k )<-aux + g.(j+k+n);
g.(j+k+n)<-aux - g.(j+k+n)
done;
if n>=2 then (
hadam j (n/2);
hadam (j+n) (n/2)
) in
hadam 0 (vect_length f / 2);
g;;
En notant ![]() le nombre d'additions et de soustractions de
complexes effectuées lors de l'appel à hadam avec
le nombre d'additions et de soustractions de
complexes effectuées lors de l'appel à hadam avec
![]() , on a
, on a ![]() , et
, et
![]() si
si
![]() ,
,
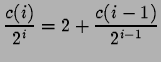 |
|
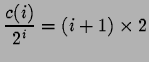 , aussi vrai pour , aussi vrai pour |